这台两千年前的计算机，为古希腊人预测日食

羊君

来源：环球科学微信公众号

　　地中海同一海域相隔两千余年的两场风暴，让古代社会最重要的技术遗物幸运地重见天日。这件“安提凯希拉装置”究竟是如何运行的，两千年前的古希腊人是怎样利用它模拟月亮的运动，甚至准确预报日食的？

　　撰文?| 托尼·弗里思（Tony Freeth）

　　翻译?| 郭凯声


        第一次风暴发生于公元前1世纪中期，一艘满载希腊珍宝的古罗马商船在风暴中葬身大海。第二次风暴则发生于公元1900年，一群在安提凯希拉岛（Antikythera，位于克里特岛与希腊本土之间的一个小岛）海域采集海绵的潜水者仓皇躲避到安全处。风暴过后，这群潜水者想碰碰运气，看能否在附近的水下找到海绵，结果意外发现那艘古罗马商船的残骸。几个月后，在希腊政府的支持下，这批潜水者回到这里。接下来的9个月里，他们发掘出一大批精美的古希腊文物，包括精美的青铜制品、玻璃器皿、酒罐、陶器以及珠宝。这是人类历史上最早的大规模水下考古发掘活动之一。

　　有件物品最初并未引起注意。这是一件已经高度钙化、大小跟电话号码簿差不多的东西。几个月后它破裂开来，露出了一些锈迹斑斑的青铜齿轮残骸，所有齿轮相互啮合在一起，齿长仅为15毫米，还有刻着专业刻度尺和希腊文字的金属板。这一发现令考古学家大为震惊，因为在那之前，大家一直认为古代人制造齿轮仅是用于粗笨的机械任务。

　　这个东西后来被称作“安提凯希拉装置”（Antikythera mechanism），有三块较大的碎片正在雅典的希腊国家考古博物馆展出。跟那些气势不凡的青铜雕像以及其他各种古希腊艺术珍品相比，这几块碎片显得非常渺小脆弱。然而它们功能之复杂却超出了所有人的想象。

　　2000年，我首次得知有这么个东西。当时我是电影制片人，英国威尔士加迪夫大学的天文学家迈克·埃德蒙兹（Mike Edmunds）找到了我，因为他觉得这个装置可以成为一部电视纪录片的极好题材。数十年来，科学家对安提凯希拉装置已经有了相当多的认识，认为它可以计算天文数据，但仍然未能完全弄清这个装置的工作原理。由于以前曾研究过数学，我逐渐对这一装置产生了强烈的兴趣。

　　我与埃德蒙兹组织起一个国际合作项目，一批历史学家和天文学家以及两组成像专家加入进来。过去几年中，我们的团队已经复原出几乎所有幸存的零件，并了解了它们的工作原理及功能。该装置可以计算月食和日食的日期，根据已有知识模拟月球在天空中复杂的视运动（apparent motion），并记录诸如奥林匹克运动会等重大社会活动的日期。就目前所知，该装置问世之后至少1000年内，世界上任何地方都不曾出现过技术复杂程度可与之媲美的东西。

公元1901年，潜水者在安提凯希拉岛附近海域的一艘沉船上发现了安提凯希拉装置的一些锈迹斑斑的碎片，上图为其中一块。

    早期的先驱

　　1905年，德国语言学家阿尔伯特·雷姆（Albert Rehm）第一个认识到，安提凯希拉装置是一台天文计算装置。半个世纪后，当美国新泽西州普林斯顿高等研究院的德里克·J·德索拉·普赖斯（Derek J。 de Solla Price）在《科学美国人》上撰文介绍这个装置时，人们仍然对它知之甚少。

　　普赖斯认为，这个装置的操作方法是转动装置侧面的曲柄，然后它会移动正面和背面各个刻度盘面上的指针，进而完成输出。使用者可以通过转动曲柄设定日期，显示在装置正面一个有365天刻度的日历盘面上。（该盘面可以通过旋转调节使日期每隔四年多一天，与现在的闰年相仿。）同时，该曲柄也驱动装置内的其他所有齿轮，使它们给出与设定日期相对应的信息。

　　装置正面的第二个盘面与日历盘面的中心相同，并被分为360度，上面还有12个代表黄道12宫星座的符号（见图安提凯希拉装置的内部）。这些星座是太阳沿一条被称为黄道（ecliptic）的路径相对于“不动的”恒星运动的过程中穿过的星座（那是当时人们的认识，其实太阳的这种“运动”是因地球绕太阳运动而产生的）。普赖斯猜想该装置正面或许有一根指针，显示指定日期太阳在黄道上的位置。

　　在遗存至今的碎片中，普赖斯找出了十几个齿轮的残骸，这些齿轮原本是该装置内部的组成部分。他还估计出了齿轮的齿数。在1974年的一项重要研究中，普赖斯描述了主要碎块中的27个齿轮，并根据希腊放射学专家哈拉兰博斯·卡拉卡洛斯（Charalambos Karakalos）对该装置进行的首次X射线扫描结果，给出了更准确的齿数估计值。

　　从齿数可以看出该装置是作什么计算用的。转动曲柄，让64齿的初级齿轮旋转一整圈，就代表经过了一年，这可以从日历盘面上的指针看出来。这个初级齿轮也同两个38齿的次级齿轮啮合成对，因此每个次级齿轮每一年转过64/38圈。同样，每一级上不同齿数的齿轮靠啮合来传递运动，传递速度由齿数比决定。最后运动传递到指针上，使指针按照一定的速率转动，而不同的速率对应于不同的天文周期。普赖斯发现，其中一个齿轮系的各齿数比正好对应于古代巴比伦的月球周期。

　　普赖斯同此前的雷姆一样，认为此装置内也有行星齿轮（epicyclic gear，也叫周转齿轮）系。

　　所谓行星齿轮，就是齿轮的轴承本身又装在其他齿轮上，就像“疯帽匠的茶杯”（迪士尼乐园的一种旋转娱乐设施）中的那些杯子。行星齿轮扩大了用齿轮可以完成的计算的范围——不仅可以计算分数乘法，还可以计算加法和减法。就现在所知，此后的1500年间，西方世界的技术中再未出现过行星齿轮的踪影。

　　还有几位研究人员也对安提凯希拉装置进行了研究，最著名的是英国伦敦科学博物馆馆长迈克尔·赖特 （Michael Wright），他与澳大利亚悉尼大学计算机科学家艾伦·布罗姆利（Allan Bromley）合作，首次对此装置进行了三维X射线测量，证明普赖斯提出的模型是错误的。布罗姆利于2002年去世，但赖特坚持不懈，研究成果显著。他找到证据证明，背面的刻度盘虽然乍看起来像是一些同心环，但其实是螺旋状的；他还发现装置正面有一个计算月相的行星齿轮机构。

　　同时赖特也采纳了普赖斯的一个观点，即装置背面上方的盘面有可能是一种基于太阴周期的月历。太阴周期以19年［235个朔望月（lunar-month），即阴历月］为一循环，又称默冬章（Metonic cycle）。这种月历以公元前5世纪雅典天文学家默冬的名字命名（其实巴比伦人在他之前已经发现了这个周期），今天仍被用来确定犹太教的新年和基督教的复活节。下面，我们还将发现该盘面上的指针是可以延伸的，这样指针尖端上的一根槽钉就可以顺着螺旋形凹槽一圈接一圈地转下去。

　　成像研究

　　当我们的团队开始研究时，资料极端缺乏。我们查不到以前的X射线扫描资料，连一套清晰点的静态照片都没有。不过，一本科学杂志上的两张图片——一张是金鱼的X射线照片，一张是巴比伦黏土板的增强照片启发了我，让我想出了一些新方法来获取更好的资料。

　　我们委托美国惠普公司完成了当时最先进的摄影成像，同时请英国的X-Tek系统公司进行三维X射线成像。经过4年耐心而谨慎的交涉和周旋，希腊亚里士多德大学的约翰·西拉扎基斯（John Seiradakis）以及雅典大学的克塞诺丰·穆萨斯（Xenophon Moussas）终于办妥了所有手续，于是我们安排成像小组带着器械前往雅典——由于安提凯希拉装置过于脆弱，不能搬动。

　　就在这时，博物馆的玛丽·扎菲罗普洛（Mary Zafeiropoulou）打来一个电话，让我们备感意外。她说她在地下仓库发现有些箱子里的东西贴着“安提凯希拉”的标签，问我们有没有兴趣。那还用说！于是，我们拥有的碎片总数一下子便从20块猛增到82块。

　　以汤姆·马尔兹本德（Tom Malzbender）为首的惠普小组安装了一个神秘的圆顶状玩意儿，直径约1.5米，上面装有一些电子闪光灯，可以从多个不同角度提供照明。该小组借用电脑游戏中一项名为“多项式纹理映射”（polynomial texture mapping）的技术来增强表面细节。普赖斯觉得很难看清的文字，现在已可清楚辨认；另外，通过调节表面的反光率和照明灯光的角度，还可以进一步增强细枝末节。这些文字其实就是写在外板上的说明书。

　　一个月后，X-Tek公司那台重达8吨的X射线扫描机“银翼杀手”（BladeRunner）运往雅典。为了让装载这台庞然大物的卡车能顺利开到博物馆，当地警方特地清空了雅典市中心的街道。银翼杀手可以进行计算机断层扫描（computed tomography，CT），与医院的CT相仿，但能更好地显示细节。X-Tek公司的罗杰·哈德兰德（Roger Hadland）及他的团队还专门改造了这台机器，以使它的X射线功率足以穿透安提凯希拉装置的碎片。这样得到的三维重构图让人惊叹不已。普赖斯只看到了让人摸不着头脑的一堆互相重叠的齿轮，而我们则能分离出碎块内部各层，并看到齿上的微小细节。

　　让人意想不到的是，X射线扫描显示，还有两千多个字符深藏在碎片内部。（原本存在的字符估计多达15 000个，现在我们已经辨认并解读出了其中3 000多个字符。）在雅典，穆萨斯与同样来自雅典大学的亚尼斯·比察基斯（Yanis Bitsakis），还有历史与古文字学研究中心的阿伽门农·采利卡斯（Agamemnon Tselikas）一起，逐步发现了两千多年来人眼一直看不见的文字。其中一段文字翻译出来是“螺旋形刻度235”，由此证明背面上方的盘面的确是表示默冬历的螺旋图案。

羊君

借助计算机断层扫描技术，研究人员复原出该装置的大部分结构

    巴比伦系统

　　回到伦敦，我便开始研究CT扫描结果。有些碎片显然都是背面下方一个螺旋形盘面的组成部分。该盘面的螺旋线绕了4圈，上面约有220~225个刻度。

　　质数223的可能性非常大。古巴比伦人已经发现，月食仅在满月期间才会发生，而一次月食发生223个月后，又会发生一次类似的月食。同样，他们还知道，日食仅发生在新月（农历初一）期间，如果观测到一次日食，他们就可以预测223个新月后会出现另一次日食（不过他们不可能次次都看到，因为日食只有某些特殊的地方才能看见，而且古代天文学家无法准确预报日食发生的地区）。日食和月食按照这种规律反复发生，因为每过223个朔望月，太阳、地球和月亮又会回到以前的排列情况，这个周期名叫沙罗周期（Saros cycle）。

　　盘面的刻度之间有一些符号块，几乎全部含有希腊字母Σ（sigma）或Η（eta），或者两者都有。我很快就明白，前一个字母代表Σεληνη（selene），即希腊语的“月亮”，表示有一次月食；后一个字母则代表Ηλιοσ（helios），即希腊语的“太阳”，表示有一次日食。巴比伦人还知道，在223个月的周期内，日食或月食只能出现在特定的月份，这些月份的分布模式可以预测，中间间隔五个或六个月。盘面上的符号也与此模式吻合。

　　现在我需要顺着这一连串线索来研究该装置的核心，看看新认识会把我们引向何方。第一步是要找出这个新沙罗盘的驱动齿轮，它应该有223个齿。卡拉卡洛斯此前估计，在主要碎块的背面上有一个大齿轮可能是222个齿。赖特将齿数修正为223，埃德蒙兹也认同这一结论。配合对其他齿轮齿数的合理估计，再加上一个假想的小齿轮，这个223齿的齿轮便可以完成需要的计算。

　　但还有一个重大问题依然无解，事实表明它也是整个齿轮系统中最难解读的一部分。除了计算沙罗周期以外，223齿的大齿轮还带有普赖斯发现的那个行星齿轮系，即两个小齿轮以类似于迪士尼茶杯游乐设施的方式安装在大齿轮上。每个行星齿轮又连接在另一个小齿轮上。让人看不懂的是，所有4个小齿轮的齿数似乎相同，都是50个齿，这看来是没有道理的，因为它意味着齿轮的输出将与输入相同。

　　有好几个月，我都一筹莫展。后来我记起赖特曾观察到那两个行星齿轮中的其中一个表面上有一根槽针插入另一个齿轮的槽中。赖特认为，这两个齿轮是绕着相距约一毫米的不同轴在旋转。因此，一个齿轮转过的角度就会忽而比另一个齿轮转过的角度大，忽而又比它小。这样，如果一个齿轮以恒定速度转动，另一个齿轮的转速就会一会儿比它略快，一会儿比它略慢，呈周期性变化。

　　异想天开

　　虽然赖特放弃了自己的看法，我却意识到这种忽快忽慢的转速恰恰就是古希腊人计算月球运动时所需要的东西。他们依据的是当时（公元前2世纪）最先进的天文理论，通常认为是罗得岛的喜帕恰斯（Hipparchos）提出的。在1609年开普勒（Kepler）发现行星运动定律之前，人们不知道月球轨道是椭圆形，当然更不知道月球在近地点（perigee，即月球离地球最近的一点）附近时速度会加快，而在远地点（apogee）附近时速度将放慢。但古人知道，月球相对于黄道带的运动似乎在周期性地减慢和加快。喜帕恰斯的模型是，月球以恒定速度绕一个圆运动，而此圆的中心又以恒定的速度绕另一个圆运动，这样就与月球视运动的实际情况非常相似了。这种叠在其他圆上的圆称为本轮（epicycle），这一理论也在以后1 800年的天文学界中占了统治地位。

　　一个因素导致问题更加复杂：远地点和近地点并不是固定不动的，因为月球的椭圆形轨道大约每9年要转动一整圈。因此，月球返回近地点所用的时间比它返回黄道带中同一点所用的时间稍长一些，两者之差为每年0.112579655转。如果输入齿轮有27个齿，大齿轮的转动幅度就稍稍大了些，而如果输入齿轮有26个齿，大齿轮的转动又稍稍小了些。正确的齿数似乎应在两者之间的中心点。因此我尝试了一种不可能的情形——26.5个齿。我按下计算器，得到的结果是0.112579655——跟正确的答案完全一样，直到小数点后第9位都完全吻合！这绝不可能是巧合，但是，齿轮的齿数不应该是分数。

　　接下来我意识到26.5×2=53。事实上，赖特已经估计到一个关键的齿轮有53个齿，此时我明白，这个齿数让所有问题迎刃而解。设计者按行星齿轮的方式布置槽针和槽，从而在保持基本转动不变的情况下巧妙地延缓了它的变化周期。这真是一个天才的构想。由于埃德蒙兹的努力，我们还意识到装置背面的行星齿轮系统带动着一根轴，而这根轴又带动另一根连接着装置正面表盘的空心轴转动，这样月球的运动就能够在黄道带盘面和月相显示上表示出来。至此，几乎所有齿轮的齿数都弄清了，但还有一个小齿轮的齿数至今仍是一个谜。

　　在进一步研究之后，我们对模型作了一些修改。其中一处修改涉及装置背面默冬历盘面内的一个较小的辅助盘面，它被分为4个象限。当我看到一个象限下面有“NEMEA”这个词时，第一条线索浮出了水面。美国纽约大学的历史学家亚历山大·琼斯 （Alexander Jones）解释说，这个词指的是奈迈阿运动会，它是古希腊5大运动会之一。最终我们识别出了刻在盘面4个象限周围的文字，其中最多的是“ISTHMIA”，它表示在科林斯举办的伊斯米亚运动会，“PYTHIA”是在德尔斐举行的皮西安运动会，“NAA”表示在多多纳举行的小型运动会，而“OLYMPIA”自然是指古希腊最重要的运动会即奥林匹克运动会了。所有运动会都是每两年或4年举行一次。以前我们认为此装置纯粹是数学天文学的工具，但是“四年周期盘”（Olympiad）——这是我们给它取的名字——却赋予该装置一种完全出乎人们意料的社会功能。

　　在30个残存的齿轮中，有29个用于计算太阳和月亮的各种周期。但是我们在研究装置正面的文字后，也得到了有关重要恒星以及行星升起和落下的大量信息。此外，在装置正面的“初级”齿轮上，残存的轴承也证明曾存在一个行星齿轮系，它的作用很可能是模拟行星沿黄道的来回运动（以及太阳自身运动的异常情况）。所有这些线索都有力地表明，此装置不仅能够模拟太阳的运动，而且至少还能模拟古代已经知道的5大行星（水星、金星、火星、木星和土星）之中部分行星的运动轨迹。

　　赖特制作了一个安提凯希拉装置的模型，它具有与所有5大行星对应的行星齿轮系。但是他的巧妙设计无法与所有证据完全吻合。而且，新模型要多出40个齿轮，结构过于复杂，无法与安提凯希拉装置现存部分那令人惊叹的简洁设计相比。最终答案恐怕仍藏在50米深的海底。

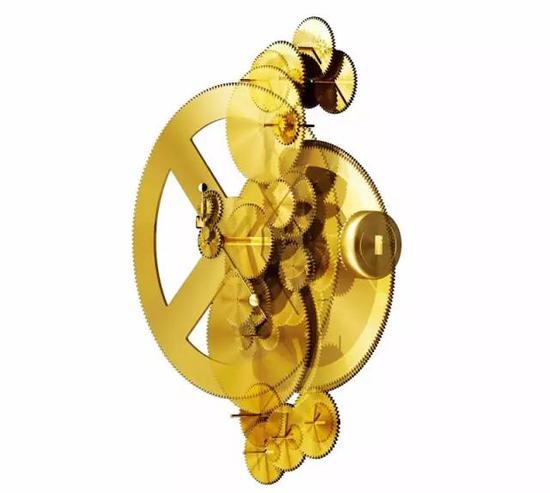
　　下面这幅安提凯希拉装置部件分解图显示了该装置已知30个齿轮中的29个，再加上一些推测的齿轮。转动装置侧面的曲柄，便可带动装置中所有齿轮一同旋转，并使装置前面和后面各盘面上的指针移动。蓝色、红色和黄色箭头显示了曲柄的运动如何从一个齿轮传递到下一个齿轮。使用者在装置正面有365天的埃及日历盘面上，或者背面有235个朔望月的默冬历盘面上选择一个日期，然后就可在其他盘面上查看该日期的天象状况，例如月球的位置及月相等。同样，你也可以通过转动曲柄在天文盘面上设定某个事件，然后再查看该事件对应的日期。

羊君

默冬齿轮系

    用于计算有235个朔望月的默冬历中的月份，并通过装置背面默冬历盘面上的指针（A）显示出来。该指针针尖上的槽针（B）沿着螺旋形凹槽移动，当指针指到依次相连的各个外圈上标示的月份时，就会逐渐变长。辅助齿轮（C）使一个较小盘面上的指针（D）转动，指示奥林匹克及其他运动会的4年周期。其他齿轮则带动另一个小盘面上的指针（E），作用可能是指示一个76年的周期。

　　月球齿轮系

　　这个系统包括若干行星齿轮，用于模拟月球运动的变化。行星齿轮装在一个较大的齿轮（A）上，宛如迪士尼乐园“疯帽匠的茶杯”游戏中的那些杯子。一个齿轮通过“槽针—槽”机构（B）使另一个齿轮转动。然后此运动通过其他齿轮传递到安提凯希拉装置正面。另一个行星齿轮系（C）带动一个半黑半白的球（D）旋转，以显示月相，而指针（E）则显示月球在黄道带盘面上的位置。

　　日月食齿轮系

　　用于计算有223个朔望月的沙罗周期中的月份（沙罗周期是日食和月食重复发生的周期）。它通过一根与默冬历盘面上的指针相仿的可延长指针（A）来显示沙罗盘面上的月份。辅助齿轮则使一个小盘面上的指针（B）移动。这根指针每过223个朔望月便转1/3圈，表示相应的月食发生时间将推迟8小时。

　　与阿基米德有缘？

　　安提凯希拉装置来自何处？它出自何人之手？这些问题仍是一个谜。那艘沉船上的货物大部分来自古希腊东部的帕加马（现土耳其境内）、科斯岛和罗得岛。人们理所当然会猜想喜帕恰斯或罗得岛的另一位天文学家设计了这个装置。但是隐藏在默冬历上235个朔望月刻度之间的文字却对这种观点提出了挑战。某些月的名称仅在古代希腊的特定地方使用，从而暗示安提凯希拉装置应该是来自科林斯。如果该装置来自科林斯本地，那么几乎可以肯定，它出现在公元前146年罗马人彻底毁掉科林斯之前。更有可能的是，安提凯希拉装置制作出来是为了在希腊西北部或西西里岛某个科林斯殖民地使用。

　　西西里岛的可能性相当大，岛上的锡拉库萨是古代最伟大的科学家阿基米德（Archimedes）居住的地方。公元前1世纪，罗马政治家西塞罗（Cicero）讲述了公元前212年阿基米德在锡拉库萨遭围攻时遇害的经过，并提到打了胜仗的罗马将领马塞勒斯（Marcellus）仅拿走了一件战利品，即阿基米德制作的一台天文仪器。会是安提凯希拉装置吗？我们认为不是，因为该装置看来是在阿基米德去世好几十年后方才问世。但它有可能是遵循阿基米德开创的仪器制作风格打造出来的。

　　普赖斯当年在《科学美国人》撰文介绍安提凯希拉装置时曾写道：

　　古希腊人在他们创造的灿烂文明即将衰落之前，竟然发展到如此接近现代水平的地步，不仅在思想方面，而且也在科学技术方面，真让我惊叹不已。

　　而我们的发现则证明，安提凯希拉装置之接近现代，甚至超过了普赖斯的想象。

煤缘

感谢分享，赵老师幸苦了！

煤缘

问好赵老师！

煤缘

祝赵老师周二快乐！

羊君

感谢白老师的回帖支持！

羊君

向敬业的白老师学习！

羊君

问好白老师！周四快乐！

羊君

问好白老师！周四快乐！